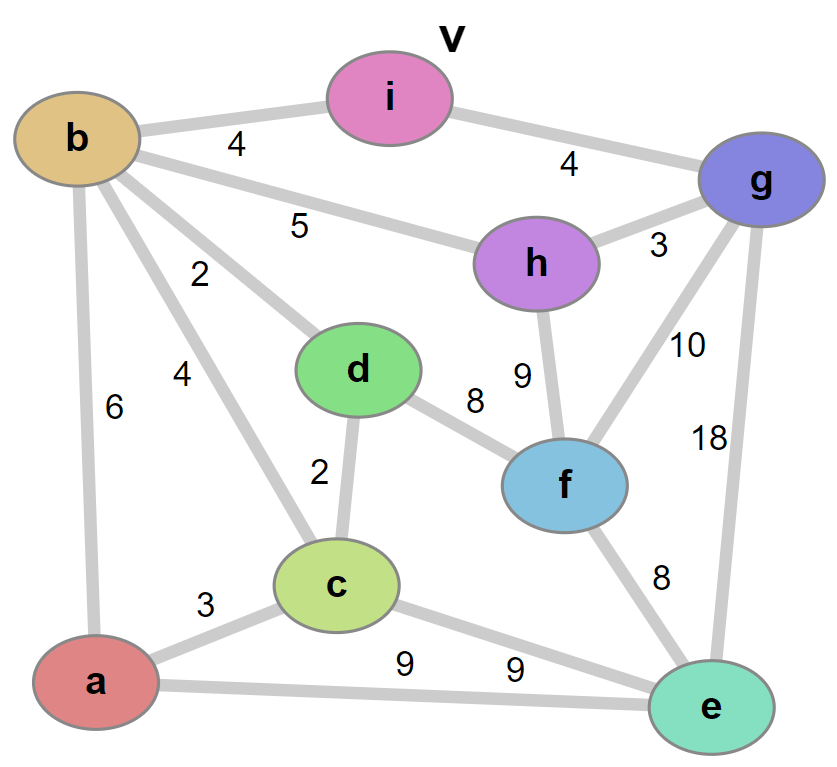
Write a C program for Kruskal’s Minimum Spanning Tree (MST) Algorithm in a Graph.
MST-Kruskal(G)
for each v ∈ G.V
Make-Set(v)
for each (u,v) by weight
if Find-Set(u) ≠ Find-Set(v)
Union(u,v)
(u,v).inMST = True
#include <stdio.h>
#include <stdlib.h>
#define MAX_VERTICES 1000
struct Edge {
int u, v, weight;
};
struct Subset {
int parent;
int rank;
};
struct Edge edges[MAX_VERTICES];
struct Subset subsets[MAX_VERTICES];
int findSet(int i) {
if (subsets[i].parent != i)
subsets[i].parent = findSet(subsets[i].parent);
return subsets[i].parent;
}
void unionSets(int x, int y) {
int xRoot = findSet(x);
int yRoot = findSet(y);
if (subsets[xRoot].rank < subsets[yRoot].rank)
subsets[xRoot].parent = yRoot;
else if (subsets[xRoot].rank > subsets[yRoot].rank)
subsets[yRoot].parent = xRoot;
else {
subsets[yRoot].parent = xRoot;
subsets[xRoot].rank++;
}
}
int compareEdges(const void *a, const void *b) {
return ((struct Edge *)a)->weight - ((struct Edge *)b)->weight;
}
void kruskalMST(struct Edge graph[], int V, int E) {
qsort(graph, E, sizeof(struct Edge), compareEdges);
for (int v = 0; v < V; v++) {
subsets[v].parent = v;
subsets[v].rank = 0;
}
int mstEdges = 0;
int mstWeight = 0;
for (int e = 0; e < E; e++) {
int u = graph[e].u;
int v = graph[e].v;
int uRoot = findSet(u);
int vRoot = findSet(v);
if (uRoot != vRoot) {
unionSets(uRoot, vRoot);
mstEdges++;
mstWeight += graph[e].weight;
printf("(%d, %d) in MST\n", u, v);
}
if (mstEdges == V - 1)
break;
}
printf("MST Weight: %d\n", mstWeight);
}
int main() {
int V, E;
printf("Enter number of vertices and edges: ");
scanf("%d %d", &V, &E);
for (int i = 0; i < E; i++) {
printf("Enter edge (u v weight): ");
scanf("%d %d %d", &edges[i].u, &edges[i].v, &edges[i].weight);
}
kruskalMST(edges, V, E);
return 0;
}
Enter number of vertices and edges: 4 5
Enter edge (u v weight):
1 2 2
1 3 3
2 3 1
2 4 4
3 4 5
Enter edge (u v weight): (2, 3) in MST
(1, 2) in MST
(2, 4) in MST
MST Weight: 7
Published by Md. Anisur Rahman
I am Md. Anisur Rahman. I have completed Cyber Security for MSCSE at United International University in 2022.I have completed PGDIT from IIT, Jahangirnagar University in 2020. I'm a Head of IT at Programming24 School.
View all posts by Md. Anisur Rahman