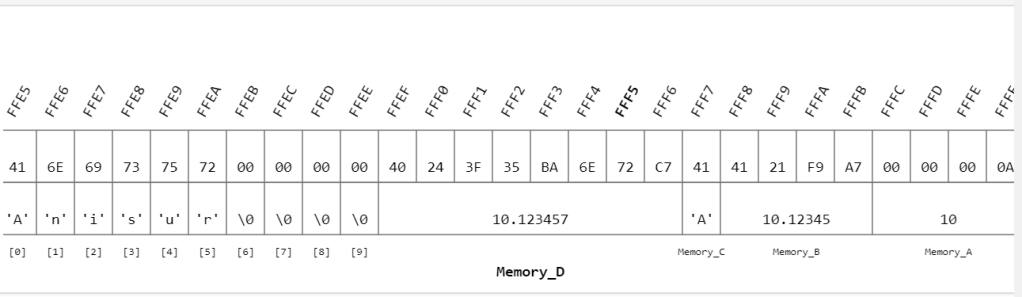
August 9, 2023August 10, 2024 Md. Anisur Rahman C Programming Lab Manual

C Programming Lab Manual – 73

Write a C program for N-Bonacci Number.

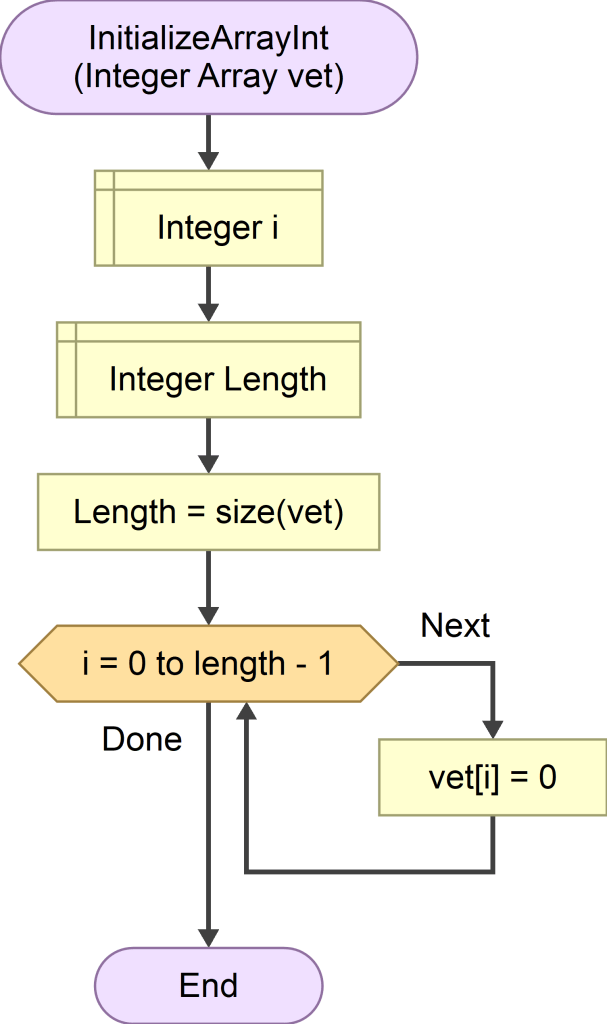
function initializeArrayInt(array, length):
    for i = 0 to length - 1:
        array[i] = 0

function bonacciseries(n, m):
    array[m]
    i = 0
    j = 0

    if m >= n:
        initializeArrayInt(array, m)
        array[n - 1] = 1
        i = n
        
        while i < m:
            j = i - n
            while j < i:
                array[i] = array[i] + array[j]
                j = j + 1
            end while
            i = i + 1
        end while
        
        i = 0
        while i < m:
            output array[i]
            output " "
            i = i + 1
        end while
        
    else:
        output "M >= N !!"
    end if

function main():
    n = 0
    m = 0

    output "N-bonacci numbers"
    output "N-bonacci number to calculate?"
    input n
    output "How many series's numbers?"
    input m
    bonacciseries(n, m)

C Programming Code

#include <stdio.h>

void initializeArrayInt(int vet[], int length) {
    int i;
    for (i = 0; i < length; i++) {
        vet[i] = 0;
    }
}

void bonacciseries(int n, int m) {
    int a[m];
    int i, j;

    if (m >= n) {
        initializeArrayInt(a, m);
        a[n - 1] = 1;
        i = n;
        while (i < m) {
            j = i - n;
            while (j < i) {
                a[i] = a[i] + a[j];
                j = j + 1;
            }
            i = i + 1;
        }
        i = 0;
        while (i < m) {
            printf("%d ", a[i]);
            i = i + 1;
        }
    } else {
        printf("M >= N !!\n");
    }
}

int main() {
    int n, m;

    printf("N-bonacci numbers\n");
    printf("N-bonacci number to calc?\n");
    scanf("%d", &n);
    printf("How many series's numbers?\n");
    scanf("%d", &m);
    bonacciseries(n, m);

    return 0;
}

N-bonacci numbers
N-bonacci number to calc?
5
How many series's numbers?
5
0 0 0 0 1

August 7, 2023August 10, 2024 Md. Anisur Rahman C Programming Lab Manual, Data Structure And Algorithm

C Programming Lab Manual – 72

Write a C program for Floyd Warshall Algorithm in a Graph.

BEGIN

 FOR ALL v ∈ V

  d[v][v] ← 0

 FOR ALL (u,v) ∈ E

  d[u][v] ← w(u,v)

 for k from 1 to |V|

  for i from 1 to |V|

   for j from 1 to |V|

    if d[i][j] > d[i][k] + d[k][j]

     d[i][j] ← d[i][k] + d[k][j]

    end if

END

C Programming Code

#include <stdio.h>
#include <limits.h>

#define V 4 // Number of vertices

void floydWarshall(int graph[V][V]) {
    int dist[V][V];

    // Initialize distance matrix
    for (int i = 0; i < V; i++) {
        for (int j = 0; j < V; j++) {
            dist[i][j] = graph[i][j];
        }
    }

    // Main algorithm
    for (int k = 0; k < V; k++) {
        for (int i = 0; i < V; i++) {
            for (int j = 0; j < V; j++) {
                if (dist[i][k] != INT_MAX && dist[k][j] != INT_MAX &&
                    dist[i][j] > dist[i][k] + dist[k][j]) {
                    dist[i][j] = dist[i][k] + dist[k][j];
                }
            }
        }
    }

    // Print the shortest distances
    printf("Shortest distances between vertices:\n");
    for (int i = 0; i < V; i++) {
        for (int j = 0; j < V; j++) {
            if (dist[i][j] == INT_MAX) {
                printf("INF ");
            } else {
                printf("%d ", dist[i][j]);
            }
        }
        printf("\n");
    }
}

int main() {
    int graph[V][V] = {
        {0, 5, INT_MAX, 10},
        {INT_MAX, 0, 3, INT_MAX},
        {INT_MAX, INT_MAX, 0, 1},
        {INT_MAX, INT_MAX, INT_MAX, 0}
    };

    floydWarshall(graph);

    return 0;
}

Shortest distances between vertices:
0 5 8 9 
INF 0 3 4 
INF INF 0 1 
INF INF INF 0

August 7, 2023August 10, 2024 Md. Anisur Rahman C Programming Lab Manual, Data Structure And Algorithm

C Programming Lab Manual – 71

Write a C program for Bellman Ford Algorithm in a Graph.

BEGIN

  d(v[1]) ← 0

  FOR j = 2,..,n DO

    d(v[j]) ← ∞

  FOR i = 1,..,(|V|-1) DO

    FOR ALL (u,v) in E DO

      d(v) ← min(d(v), d(u)+l(u,v))

  FOR ALL (u,v) in E DO

    IF d(v) > d(u) + l(u,v) DO

      Message: "Negative Circle"

END

C Programming Code

#include <stdio.h>
#include <limits.h>

#define MAX_VERTICES 100
#define MAX_EDGES 100

typedef struct {
    int u, v, weight;
} Edge;

int numVertices, numEdges;
int distance[MAX_VERTICES];
Edge edges[MAX_EDGES];

void bellmanFord(int startVertex) {
    distance[startVertex] = 0;

    for (int j = 1; j <= numVertices; j++) {
        if (j != startVertex) {
            distance[j] = INT_MAX;
        }
    }

    for (int i = 1; i <= numVertices - 1; i++) {
        for (int k = 0; k < numEdges; k++) {
            int u = edges[k].u;
            int v = edges[k].v;
            int weight = edges[k].weight;

            if (distance[u] != INT_MAX && distance[u] + weight < distance[v]) {
                distance[v] = distance[u] + weight;
            }
        }
    }

    for (int k = 0; k < numEdges; k++) {
        int u = edges[k].u;
        int v = edges[k].v;
        int weight = edges[k].weight;

        if (distance[u] != INT_MAX && distance[u] + weight < distance[v]) {
            printf("Negative Circle\n");
            return;
        }
    }
}

int main() {
    scanf("%d %d", &numVertices, &numEdges);

    for (int i = 0; i < numEdges; i++) {
        scanf("%d %d %d", &edges[i].u, &edges[i].v, &edges[i].weight);
    }

    int startVertex;
    scanf("%d", &startVertex);

    bellmanFord(startVertex);

    for (int i = 1; i <= numVertices; i++) {
        printf("Vertex %d: Distance = %d\n", i, distance[i]);
    }

    return 0;
}

5 8
1 2 3
1 3 6
2 3 -2
2 4 5
3 4 4
3 5 2
4 2 -7
5 4 1
1
Negative Circle
Vertex 1: Distance = 0
Vertex 2: Distance = -17
Vertex 3: Distance = -14
Vertex 4: Distance = -11
Vertex 5: Distance = -12

August 6, 2023August 10, 2024 Md. Anisur Rahman C Programming Lab Manual, Data Structure And Algorithm

C Programming Lab Manual – 70

Write a C program for Dijkstra Algorithm in a Graph.

Dijkstra(G,s):
	 for each vertex u ∈ G.V - {s}
	 u.d = ∞
	 u.pred = null
	 u.done = false
	 s.d = 0
	Q = G.V
	 while Q ≠ ∅
	 u = Q.extractMin()
	 u.done = true
	 for each v ∈ G.Adj[u]
	 Relax(u,v)
Relax(G,u,v):
	if u.d + G.edge(u,v).w < v.d
	 v.d = u.d + G.edge(u,v).w
	v.pred = u

C Programming Code

#include <stdio.h>
#include <stdlib.h>
#include <limits.h>

#define MAX_VERTICES 1000

struct Edge {
    int v;
    int weight;
    struct Edge *next;
};

struct Vertex {
    int d;
    int pred;
    int done;
    struct Edge *adjList;
};

struct Vertex vertices[MAX_VERTICES];
int numVertices;

void relax(int u, int v, int weight) {
    if (vertices[u].d + weight < vertices[v].d) {
        vertices[v].d = vertices[u].d + weight;
        vertices[v].pred = u;
    }
}

int extractMin(int Q[]) {
    int min = INT_MAX;
    int minIndex = -1;

    for (int i = 0; i < numVertices; i++) {
        if (!vertices[i].done && vertices[i].d < min) {
            min = vertices[i].d;
            minIndex = i;
        }
    }

    return minIndex;
}

void dijkstra(int source) {
    for (int u = 0; u < numVertices; u++) {
        vertices[u].d = INT_MAX;
        vertices[u].pred = -1;
        vertices[u].done = 0;
    }

    vertices[source].d = 0;

    int Q[MAX_VERTICES];
    for (int i = 0; i < numVertices; i++) {
        Q[i] = i;
    }

    while (1) {
        int u = extractMin(Q);
        if (u == -1) break;

        vertices[u].done = 1;
        
        struct Edge *edge = vertices[u].adjList;
        while (edge != NULL) {
            relax(u, edge->v, edge->weight);
            edge = edge->next;
        }
    }
}

int main() {
    int numEdges;
    printf("Enter the number of vertices and edges: ");
    scanf("%d %d", &numVertices, &numEdges);

    for (int i = 0; i < numVertices; i++) {
        vertices[i].adjList = NULL;
    }

    printf("Enter edge information (u v weight):\n");
    for (int i = 0; i < numEdges; i++) {
        int u, v, weight;
        scanf("%d %d %d", &u, &v, &weight);

        struct Edge *newEdge = malloc(sizeof(struct Edge));
        newEdge->v = v;
        newEdge->weight = weight;
        newEdge->next = vertices[u].adjList;
        vertices[u].adjList = newEdge;
    }

    int source;
    printf("Enter the source vertex: ");
    scanf("%d", &source);

    dijkstra(source);

    printf("Shortest paths from source vertex %d:\n", source);
    for (int i = 0; i < numVertices; i++) {
        if (i != source) {
            printf("Vertex %d: Distance = %d, Pred = %d\n", i, vertices[i].d, vertices[i].pred);
        }
    }

    return 0;
}

Enter the number of vertices and edges: 5 7
Enter edge information (u v weight):
0 1 4
0 2 1
1 2 3
1 3 2
2 3 4
2 4 5
3 4 1
Enter the source vertex: 0
Shortest paths from source vertex 0:
Vertex 1: Distance = 4, Pred = 0
Vertex 2: Distance = 1, Pred = 0
Vertex 3: Distance = 5, Pred = 2
Vertex 4: Distance = 6, Pred = 2

August 6, 2023August 10, 2024 Md. Anisur Rahman C Programming Lab Manual, Data Structure And Algorithm

C Programming Lab Manual – 69

Write a C program for Kruskal’s Minimum Spanning Tree (MST) Algorithm in a Graph.

MST-Kruskal(G)
	    for each v ∈ G.V
 Make-Set(v)
	   for each (u,v) by weight
if Find-Set(u) ≠ Find-Set(v)
Union(u,v)
(u,v).inMST = True

C Programming Code

#include <stdio.h>
#include <stdlib.h>

#define MAX_VERTICES 1000

struct Edge {
    int u, v, weight;
};

struct Subset {
    int parent;
    int rank;
};

struct Edge edges[MAX_VERTICES];
struct Subset subsets[MAX_VERTICES];

int findSet(int i) {
    if (subsets[i].parent != i)
        subsets[i].parent = findSet(subsets[i].parent);
    return subsets[i].parent;
}

void unionSets(int x, int y) {
    int xRoot = findSet(x);
    int yRoot = findSet(y);

    if (subsets[xRoot].rank < subsets[yRoot].rank)
        subsets[xRoot].parent = yRoot;
    else if (subsets[xRoot].rank > subsets[yRoot].rank)
        subsets[yRoot].parent = xRoot;
    else {
        subsets[yRoot].parent = xRoot;
        subsets[xRoot].rank++;
    }
}

int compareEdges(const void *a, const void *b) {
    return ((struct Edge *)a)->weight - ((struct Edge *)b)->weight;
}

void kruskalMST(struct Edge graph[], int V, int E) {
    qsort(graph, E, sizeof(struct Edge), compareEdges);

    for (int v = 0; v < V; v++) {
        subsets[v].parent = v;
        subsets[v].rank = 0;
    }

    int mstEdges = 0;
    int mstWeight = 0;

    for (int e = 0; e < E; e++) {
        int u = graph[e].u;
        int v = graph[e].v;

        int uRoot = findSet(u);
        int vRoot = findSet(v);

        if (uRoot != vRoot) {
            unionSets(uRoot, vRoot);
            mstEdges++;
            mstWeight += graph[e].weight;
            printf("(%d, %d) in MST\n", u, v);
        }

        if (mstEdges == V - 1)
            break;
    }

    printf("MST Weight: %d\n", mstWeight);
}

int main() {
    int V, E;
    printf("Enter number of vertices and edges: ");
    scanf("%d %d", &V, &E);

    for (int i = 0; i < E; i++) {
        printf("Enter edge (u v weight): ");
        scanf("%d %d %d", &edges[i].u, &edges[i].v, &edges[i].weight);
    }

    kruskalMST(edges, V, E);

    return 0;
}

Enter number of vertices and edges: 4 5
Enter edge (u v weight): 
1 2 2
1 3 3
2 3 1
2 4 4
3 4 5
Enter edge (u v weight): (2, 3) in MST
(1, 2) in MST
(2, 4) in MST
MST Weight: 7

August 5, 2023August 10, 2024 Md. Anisur Rahman C Programming Lab Manual, Data Structure And Algorithm

C Programming Lab Manual – 68

Write a C program for Prims’s Minimum Spanning Tree (MST) Algorithm in a Graph.

MST-Prim(G,r)
for each u ∈ G.V
       u.key = ∞
	   u.pred = nil
	   r.key = 0
	   Q = G.V
while Q ≠ ∅
	 u = ExtractMin(Q)
	 for each v ∈ G.Adj[u]
	 if v ∈ Q and w(u,v) < v.key
	 v.pred = u
	 v.key = w(u,v)

C Programming Code

#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#include <limits.h>

// Define the maximum number of vertices in the graph
#define MAX_VERTICES 100

// Structure to represent a vertex
struct Vertex {
    int key;
    int pred;
};

// Function to extract the vertex with the minimum key from the queue
int extractMin(struct Vertex Q[], int size, bool visited[]) {
    int minIndex = -1;
    int minValue = INT_MAX;
    
    for (int i = 0; i < size; i++) {
        if (!visited[i] && Q[i].key < minValue) {
            minValue = Q[i].key;
            minIndex = i;
        }
    }
    
    return minIndex;
}

// Main Prim's algorithm function
void MST_Prim(int G[MAX_VERTICES][MAX_VERTICES], int numVertices, int r) {
    struct Vertex vertices[MAX_VERTICES];
    bool visited[MAX_VERTICES] = {false};
    
    // Initialize vertices
    for (int u = 0; u < numVertices; u++) {
        vertices[u].key = INT_MAX;
        vertices[u].pred = -1;
    }
    
    vertices[r].key = 0;
    
    for (int i = 0; i < numVertices; i++) {
        int u = extractMin(vertices, numVertices, visited);
        visited[u] = true;
        
        for (int v = 0; v < numVertices; v++) {
            if (G[u][v] && !visited[v] && G[u][v] < vertices[v].key) {
                vertices[v].pred = u;
                vertices[v].key = G[u][v];
            }
        }
    }
    
    // Print the minimum spanning tree
    printf("Edge   Weight\n");
    for (int i = 0; i < numVertices; i++) {
        if (vertices[i].pred != -1) {
            printf("%d - %d   %d\n", vertices[i].pred, i, vertices[i].key);
        }
    }
}

int main() {
    int numVertices, r;
    int G[MAX_VERTICES][MAX_VERTICES];
    
    printf("Enter the number of vertices: ");
    scanf("%d", &numVertices);
    
    printf("Enter the adjacency matrix:\n");
    for (int i = 0; i < numVertices; i++) {
        for (int j = 0; j < numVertices; j++) {
            scanf("%d", &G[i][j]);
        }
    }
    
    printf("Enter the root vertex: ");
    scanf("%d", &r);
    
    MST_Prim(G, numVertices, r);
    
    return 0;
}

Enter the number of vertices: 5
Enter the adjacency matrix:
0 2 0 6 0
2 0 3 8 5
0 3 0 0 7
6 8 0 0 9
0 5 7 9 0
Enter the root vertex: 0
Edge   Weight
0 - 1   2
1 - 2   3
0 - 3   6
1 - 4   5

August 5, 2023August 10, 2024 Md. Anisur Rahman C Programming Lab Manual, Data Structure And Algorithm

C Programming Lab Manual – 67

Write a C program for Depth-First-Search (DFS) in a Graph.

DFS(G):
	  for each u ∈ G.V
      u.color = white
      time = 0
	  for each u ∈ G.V
	  if u.color == white
	  DFS-Visit(G,u)

DFS-Visit(G,u):
	 u.d = ++time
	 u.color = gray
	 for each v ∈ G.Adj[u]
	 if v.color == white
	 DFS-Visit(G,v)
     u.color = black
	 u.f = ++time

C Programming Code

#include <stdio.h>
#include <stdlib.h>

#define MAX_NODES 5

typedef struct Node {
    int value;
    int color;
    int d;
    int f;
} Node;

void DFS(Node graph[], int u, int *time) {
    graph[u].color = 1;
    graph[u].d = ++(*time);

    for (int i = 0; i < MAX_NODES; i++) {
        if (graph[u].color == 0 && graph[u].value != graph[i].value) {
            DFS(graph, i, time);
        }
    }

    graph[u].color = 2;
    graph[u].f = ++(*time);
}

int main() {
    Node graph[MAX_NODES] = {
        {0, 0, 0, 0},
        {1, 0, 0, 0},
        {2, 0, 0, 0},
        {3, 0, 0, 0},
        {4, 0, 0, 0}
    };

    int adjacencyMatrix[MAX_NODES][MAX_NODES] = {
        {0, 1, 1, 0, 0},
        {0, 0, 0, 1, 1},
        {0, 0, 0, 0, 1},
        {0, 0, 0, 0, 0},
        {0, 0, 0, 0, 0}
    };

    int time = 0;

    for (int i = 0; i < MAX_NODES; i++) {
        if (graph[i].color == 0) {
            DFS(graph, i, &time);
        }
    }

    printf("Node\tColor\tDiscovery Time\tFinish Time\n");
    for (int i = 0; i < MAX_NODES; i++) {
        printf("%d\t%d\t%d\t%d\n", graph[i].value, graph[i].color, graph[i].d, graph[i].f);
    }

    return 0;
}

Node	Color	Discovery Time	Finish Time
0	2	1	        2
1	2	3	        4
2	2	5	        6
3	2	7	        8
4	2	9	        10

August 5, 2023August 10, 2024 Md. Anisur Rahman C Programming Lab Manual, Data Structure And Algorithm

C Programming Lab Manual – 66

Write a C program for Breadth-First-Search (BFS) in a Graph.

for each u ∈ G.V - {s}
              u.color = white
s.color = gray
s.d = 0
Q = ∅
Q.enqueue(s)
while Q ≠ ∅
	      u = Q.dequeue()
         for each v ∈ G.Adj[u]
	           if v.color == white
	                  v.color = gray
	                  v.d = u.d + 1
	                  v.pred = u
	                  Q.enqueue(v)
	         u.color = black

C Programming Code

#include <stdio.h>
#include <stdlib.h>

#define MAX_NODES 5

// Structure to represent a node in the graph
typedef struct Node {
    int value;
    int color; // 0: white, 1: gray, 2: black
    int d;     // Distance from source
    struct Node* pred; // Predecessor in BFS traversal
    struct Node* next; // Linked list of adjacent nodes
} Node;

// Queue structure
typedef struct Queue {
    Node* items[MAX_NODES];
    int front;
    int rear;
} Queue;

void enqueue(Queue* q, Node* node) {
    q->items[q->rear++] = node;
}

Node* dequeue(Queue* q) {
    return q->items[q->front++];
}

// Breadth-First Search function
void BFS(Node* graph[], int numNodes, Node* source) {
    Queue q;
    q.front = 0;
    q.rear = 0;

    // Initialize the queue and source node
    enqueue(&q, source);
    source->color = 1; // Gray
    source->d = 0;
    source->pred = NULL;

    while (q.front != q.rear) {
        Node* u = dequeue(&q);
        Node* v = u->next;

        while (v != NULL) {
            if (v->color == 0) { // White
                v->color = 1; // Gray
                v->d = u->d + 1;
                v->pred = u;
                enqueue(&q, v);
            }
            v = v->next;
        }

        u->color = 2; // Black
    }
}

int main() {
    // Create nodes
    Node* nodes[MAX_NODES];
    for (int i = 0; i < MAX_NODES; i++) {
        nodes[i] = (Node*)malloc(sizeof(Node));
        nodes[i]->value = i;
        nodes[i]->color = 0; // White
        nodes[i]->d = -1;    // Distance uninitialized
        nodes[i]->pred = NULL;
        nodes[i]->next = NULL;
    }

    // Add edges (Modify this part to match your graph)
    nodes[0]->next = nodes[1];
    nodes[1]->next = nodes[2];
    nodes[2]->next = nodes[3];
    nodes[3]->next = nodes[4];

    // Perform BFS
    BFS(nodes, MAX_NODES, nodes[0]);

    // Print results
    for (int i = 0; i < MAX_NODES; i++) {
        printf("Node %d: Color: %d, Distance: %d\n", nodes[i]->value, nodes[i]->color, nodes[i]->d);
    }

    // Free allocated memory
    for (int i = 0; i < MAX_NODES; i++) {
        free(nodes[i]);
    }

    return 0;
}

Node 0: Color: 2, Distance: 0
Node 1: Color: 2, Distance: 1
Node 2: Color: 2, Distance: 1
Node 3: Color: 2, Distance: 1
Node 4: Color: 2, Distance: 1

August 3, 2023August 10, 2024 Md. Anisur Rahman C Programming Lab Manual

C Programming Lab Manual – 65

Write a C program for Memory Allocation using Bytes and Bits.

1. Include the standard input/output library. 
2. Define the main function.
   1. Declare variables: Memory_A as integer, Memory_B as float,
      Memory_C as char, Memory_D as double, Memory_Str as String.
   2. Print a comment to show memory state.
   3. Assign the value 10 to Memory_A.
   4. Assign the value 10.12345 to Memory_B.
   5. Assign the character 'A' to Memory_C.
   6. Assign the value 10.123456789 to Memory_D.
   7. Assign the string "Anisur" to Memory_Str.
   8. Print the size of Memory_A in bytes or bits.
   9. Print the size of Memory_B in bytes or bits.
   10. Print the size of Memory_C in bytes or bits.
   11. Print the size of Memory_D in bytes or bits.
   12. Print the size of Memory_Str in bytes or bits.
   13. End the main function and return 0.
3. End of program.

C Programming Code

#include <stdio.h>

int main()
{
    //!showMemory()
    int Memory_A = 10;
    float Memory_B = 10.12345;
    char Memory_C = 'A';
    double Memory_D = 10.123456789;
    char Memory_Str[10] = "Anisur";
    
    printf("The size of Memory of int, Memory_A = %zu Bytes or %lu bits\n",sizeof(Memory_A),sizeof(Memory_A)*8);
    printf("The size of Memory of float, Memory_B = %zu Bytes or %lu bits\n",sizeof(Memory_B),sizeof(Memory_B)*8);
    printf("The size of Memory of char, Memory_C = %zu Bytes or %lu bits\n",sizeof(Memory_C),sizeof(Memory_C)*8);
    printf("The size of Memory of double, Memory_A = %zu Bytes or %lu bits\n",sizeof(Memory_D),sizeof(Memory_D)*8);
    printf("The size of Memory of Str, Memory_Str = %zu Bytes or %lu bits\n",sizeof(Memory_Str),sizeof(Memory_Str)*8);
    return 0;
}

The size of Memory of int, Memory_A = 4 Bytes or 32 bits
The size of Memory of float, Memory_B = 4 Bytes or 32 bits
The size of Memory of char, Memory_C = 1 Bytes or 8 bits
The size of Memory of double, Memory_A = 8 Bytes or 64 bits
The size of Memory of Str, Memory_Str = 10 Bytes or 80 bits

May 21, 2023August 10, 2024 Md. Anisur Rahman C Programming Lab Manual, Data Structure And Algorithm

C Programming Lab Manual – 64

Write a C program for Binary Tree Traversal to in-order, Pre-Order, And Post-Order.

Node:
  item
  left
  right

InorderTraversal(node):
  if node is null, return
  InorderTraversal(node.left)
  Print node.item
  InorderTraversal(node.right)

PreorderTraversal(node):
  if node is null, return
  Print node.item
  PreorderTraversal(node.left)
  PreorderTraversal(node.right)

PostorderTraversal(node):
  if node is null, return
  PostorderTraversal(node.left)
  PostorderTraversal(node.right)
  Print node.item

CreateNode(value):
  newNode = new Node
  newNode.item = value
  newNode.left = null
  newNode.right = null
  return newNode

InsertLeft(parent, value):
  parent.left = CreateNode(value)
  return parent.left

InsertRight(parent, value):
  parent.right = CreateNode(value)
  return parent.right

Main:
  root = CreateNode(1)
  leftNode = InsertLeft(root, 12)
  rightNode = InsertRight(root, 9)

  InsertLeft(leftNode, 5)
  InsertRight(leftNode, 6)

  Print "Inorder traversal:"
  InorderTraversal(root)

  Print "\nPreorder traversal:"
  PreorderTraversal(root)

  Print "\nPostorder traversal:"
  PostorderTraversal(root)

C Programming Code

#include <stdio.h>
#include <stdlib.h>

struct node {
  int item;
  struct node* left;
  struct node* right;
};

// Tree traversal functions
void inorderTraversal(struct node* root) {
  if (root == NULL) return;
  inorderTraversal(root->left);
  printf("%d -> ", root->item);
  inorderTraversal(root->right);
}

void preorderTraversal(struct node* root) {
  if (root == NULL) return;
  printf("%d -> ", root->item);
  preorderTraversal(root->left);
  preorderTraversal(root->right);
}

void postorderTraversal(struct node* root) {
  if (root == NULL) return;
  postorderTraversal(root->left);
  postorderTraversal(root->right);
  printf("%d -> ", root->item);
}

// Create a new Node
struct node* createNode(int value) {
  struct node* newNode = malloc(sizeof(struct node));
  newNode->item = value;
  newNode->left = NULL;
  newNode->right = NULL;
  return newNode;
}

// Insert a node on the left of the parent node
struct node* insertLeft(struct node* parent, int value) {
  parent->left = createNode(value);
  return parent->left;
}

// Insert a node on the right of the parent node
struct node* insertRight(struct node* parent, int value) {
  parent->right = createNode(value);
  return parent->right;
}

int main() {
  //!showMemory() 
  struct node* root = createNode(1);
  struct node* leftNode = insertLeft(root, 12);
  struct node* rightNode = insertRight(root, 9);

  insertLeft(leftNode, 5);
  insertRight(leftNode, 6);

  printf("Inorder traversal:\n");
  inorderTraversal(root);

  printf("\n\nPreorder traversal:\n");
  preorderTraversal(root);

  printf("\n\nPostorder traversal:\n");
  postorderTraversal(root);

  return 0;
}

Inorder traversal:
5 -> 12 -> 6 -> 1 -> 9 -> 

Preorder traversal:
1 -> 12 -> 5 -> 6 -> 9 -> 

Postorder traversal:
5 -> 6 -> 12 -> 9 -> 1 ->

Design a site like this with WordPress.com