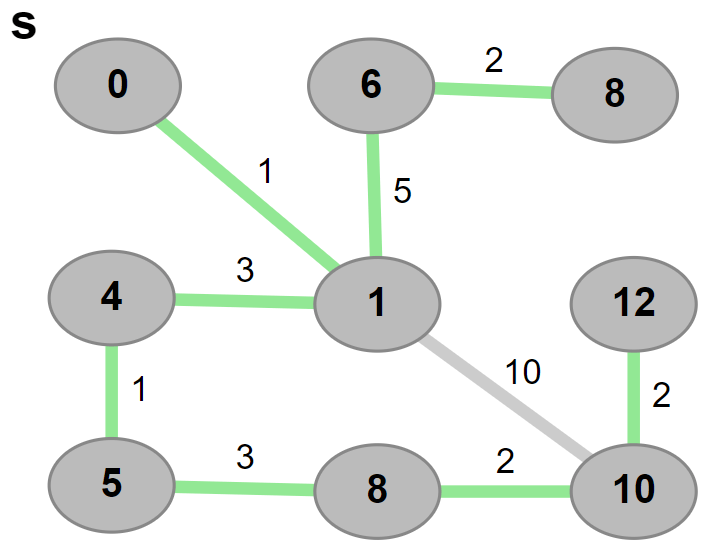
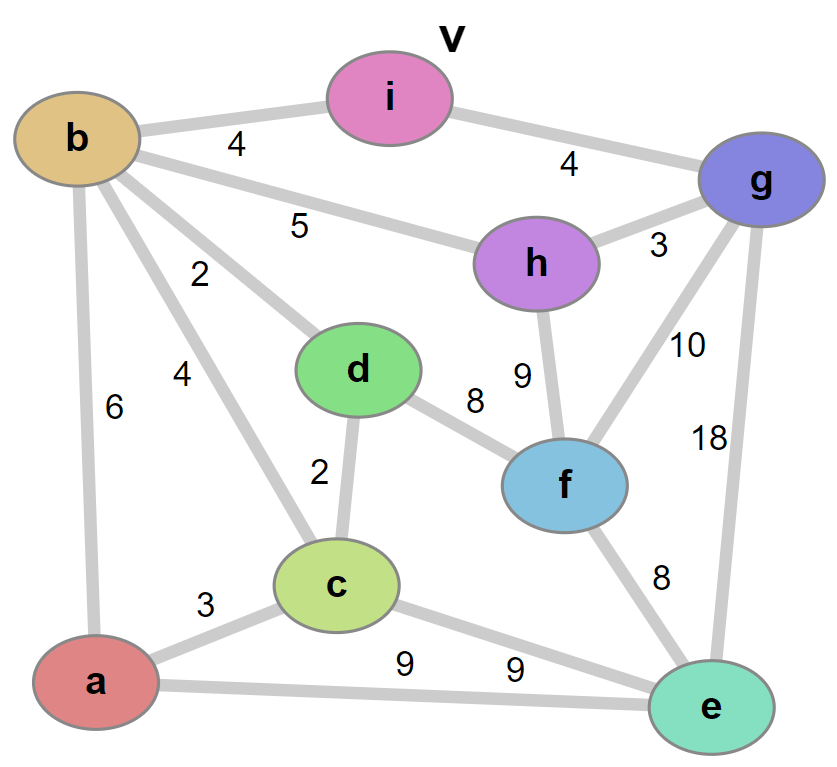
Write a C program for Dijkstra Algorithm in a Graph.
Dijkstra(G,s):
for each vertex u ∈ G.V - {s}
u.d = ∞
u.pred = null
u.done = false
s.d = 0
Q = G.V
while Q ≠ ∅
u = Q.extractMin()
u.done = true
for each v ∈ G.Adj[u]
Relax(u,v)
Relax(G,u,v):
if u.d + G.edge(u,v).w < v.d
v.d = u.d + G.edge(u,v).w
v.pred = u
#include <stdio.h>
#include <stdlib.h>
#include <limits.h>
#define MAX_VERTICES 1000
struct Edge {
int v;
int weight;
struct Edge *next;
};
struct Vertex {
int d;
int pred;
int done;
struct Edge *adjList;
};
struct Vertex vertices[MAX_VERTICES];
int numVertices;
void relax(int u, int v, int weight) {
if (vertices[u].d + weight < vertices[v].d) {
vertices[v].d = vertices[u].d + weight;
vertices[v].pred = u;
}
}
int extractMin(int Q[]) {
int min = INT_MAX;
int minIndex = -1;
for (int i = 0; i < numVertices; i++) {
if (!vertices[i].done && vertices[i].d < min) {
min = vertices[i].d;
minIndex = i;
}
}
return minIndex;
}
void dijkstra(int source) {
for (int u = 0; u < numVertices; u++) {
vertices[u].d = INT_MAX;
vertices[u].pred = -1;
vertices[u].done = 0;
}
vertices[source].d = 0;
int Q[MAX_VERTICES];
for (int i = 0; i < numVertices; i++) {
Q[i] = i;
}
while (1) {
int u = extractMin(Q);
if (u == -1) break;
vertices[u].done = 1;
struct Edge *edge = vertices[u].adjList;
while (edge != NULL) {
relax(u, edge->v, edge->weight);
edge = edge->next;
}
}
}
int main() {
int numEdges;
printf("Enter the number of vertices and edges: ");
scanf("%d %d", &numVertices, &numEdges);
for (int i = 0; i < numVertices; i++) {
vertices[i].adjList = NULL;
}
printf("Enter edge information (u v weight):\n");
for (int i = 0; i < numEdges; i++) {
int u, v, weight;
scanf("%d %d %d", &u, &v, &weight);
struct Edge *newEdge = malloc(sizeof(struct Edge));
newEdge->v = v;
newEdge->weight = weight;
newEdge->next = vertices[u].adjList;
vertices[u].adjList = newEdge;
}
int source;
printf("Enter the source vertex: ");
scanf("%d", &source);
dijkstra(source);
printf("Shortest paths from source vertex %d:\n", source);
for (int i = 0; i < numVertices; i++) {
if (i != source) {
printf("Vertex %d: Distance = %d, Pred = %d\n", i, vertices[i].d, vertices[i].pred);
}
}
return 0;
}
Enter the number of vertices and edges: 5 7